滑轮导轨宽度计算 - 一次计算机性能滥用记录

闲的没事干

起因

竞赛的机械装置 (圆柱) 需要垂直转动, 使用伺服电机控制转向. 为了使电机运动顺畅, 同时防止装置转到时 碰到离得很近的外侧装置 (圆环柱), 我采用了 H 槽滑轮 + 木板导轨的形式. 为了确定 选定尺寸的滑轮 是否可以在导轨上顺畅运行而不会脱轨 / 卡住, 需要计算导轨在不同宽度下的最小半径.

抽象化问题

滑轮选择如图所示, 半径 20, 内槽宽 12.

导轨外半径不能超过 55, 同时滑轮决定了最大宽度不能超过 12.
木板厚度为 3, 无需考虑.
于是用中学的知识, 得到木板在轮子内部的长度为 $2\sqrt{111}$.

中午告诉了🐯同学方案, 他很感兴趣, 于是加入一起解决问题 =D
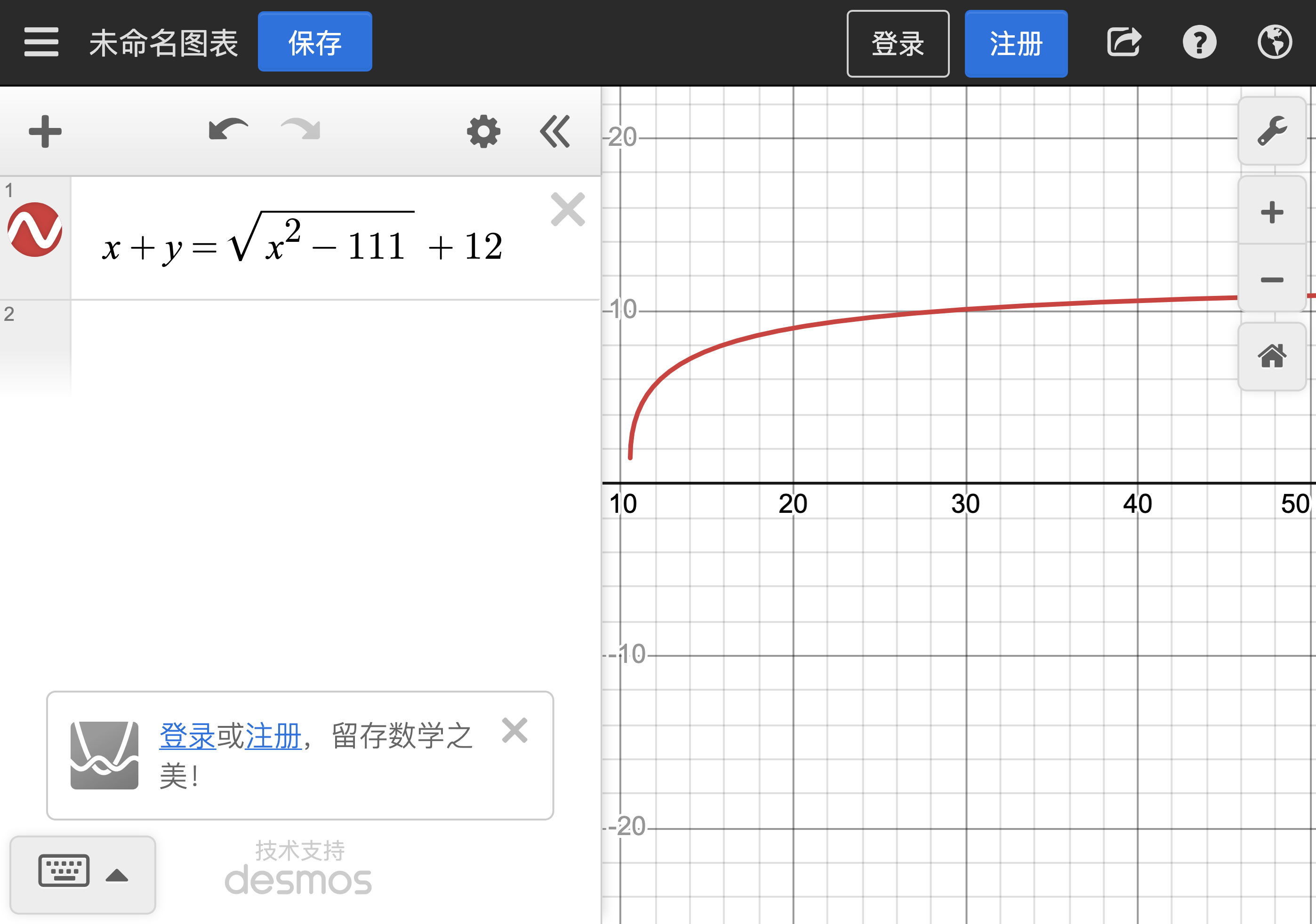
接着查看俯视图 (两条横线就是滑轮的两个凸轮缘), 设导轨内半径为 x, 导轨宽度为 y, 得到 $x+y=\sqrt{x^2-111}+12$.

笑死, 当时两个人都把直径半径搞错了 (更正处). 而且直到最后一步我都没发现这个问题

用计算机解方程 (原始)

列不出更多方程了, 🐯同学放弃了解方程.
不过我有 python, 而且相信力大砖飞 (感觉稍加优化后数据量并不大).
打开电脑问了问 DeepSeek, 写了个程序.

写一个 python 程序, 要求定义变量x和y, 满足方程”x+y=\sqrt{x^2-111}+12”, 且 x+y 小于 110. 给定 y, 使用指定的方法算出 x 的最小可能值, 精确到两位小数. 方法: 从 \sqrt{111} 开始, 到 110-y 的所有整数带入 x, 与给定的 y 值算出左右边相差, 选择最小的那个对应的 x 值的整数区间, 步进 0.001 依次带入计算左右边相差, 取最小的输出此时的 x 值.

为了实现这个程序，我们需要按照以下步骤进行：

1. 定义变量 x 和 y。
2. 使用给定的 y 值，从 sqrt(111) 开始到 110 - y 的所有整数带入 x，计算方程两边的差值。
3. 找到差值最小的 x 值的整数区间。
4. 在这个区间内，以步进 0.001 的方式带入 x，计算方程两边的差值，找到最小的差值对应的 x 值。
5. 输出 x 的最小可能值，精确到两位小数。

以下是实现这个程序的 Python 代码：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42

>import math >def find_min_x(y): min_diff = float('inf') best_x = 0.0 # 从 sqrt(111) 开始到 110 - y 的所有整数带入 x start_x = int(math.sqrt(111)) end_x = int(110 - y) # 遍历整数区间 for x_int in range(start_x, end_x + 1): # 计算方程两边的差值 left_side = x_int + y right_side = math.sqrt(x_int**2 - 111) + 12 diff = abs(left_side - right_side) # 找到差值最小的 x 值的整数区间 if diff < min_diff: min_diff = diff best_x_int = x_int # 在 best_x_int 的附近以步进 0.001 的方式带入 x for x in range(int(best_x_int * 1000), int((best_x_int + 1) * 1000)): x_val = x / 1000.0 left_side = x_val + y right_side = math.sqrt(x_val**2 - 111) + 12 diff = abs(left_side - right_side) # 找到最小的差值对应的 x 值 if diff < min_diff: min_diff = diff best_x = x_val return round(best_x, 2) ># 给定 y 值 >y = 50 # 你可以根据需要修改 y 的值 ># 计算并输出 x 的最小可能值 >x_min = find_min_x(y) >print(f"x 的最小可能值是: {x_min}")

代码说明：

1. find_min_x(y) 函数用于计算给定 y 值时的最小 x 值。
2. start_x 和 end_x 分别表示 x 的整数区间的起始和结束值。
3. min_diff 用于记录最小的差值，**best_x** 用于记录对应的 x 值。
4. 在整数区间内遍历 x，计算方程两边的差值，并找到差值最小的 x 值的整数区间。
5. 在找到的整数区间内，以步进 0.001 的方式遍历 x，计算方程两边的差值，并找到最小的差值对应的 x 值。
6. 最后返回 x 的最小可能值，精确到两位小数。

示例输出：

假设 y = 50，程序将输出 x 的最小可能值。

1	>x 的最小可能值是: 10.12

你可以根据需要修改 y 的值来得到不同的结果。

其实之前问了好几遍了, 都用的二分法, 但是得出的结果要么最小, 要么最大. Debug 一下发现这个方程用不了二分法解 (左右相差绝对值会单调增加).
本着 当今计算机性能严重过剩 的信条, 就出现了文中的选择枚举法.
反正只跑一次, 不缺时间.jpg

程序改进

为了保险 (其实就是懒得优化)

1. (这是真的优化) 因为误差绝对值单调增加, 所以下一个 左右边差值 大于 最小差值 直接 break.
2. 整数附近 0.001 步进枚举的范围增加了一些, 开始的整数减 2, 结束整数加 2.
3. 精确枚举时如果到最后 左右边差值 还是大于 0.01 (意味着还需要增加 x), 输出 -1 (满足不了).
4. for 循环输出当 y 为 10 和 12 步进 0.1 的每一个解, 用 format 做了一个简易表格.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

import math


def find_min_x(y):
    min_diff = float('inf')
    best_x = 0.0

    # 从 sqrt(111) 开始到 110 - y 的所有整数带入 x
    start_x = int(math.sqrt(111)) + 1
    end_x = int(55 - y)

    # 遍历整数区间
    for x_int in range(start_x, end_x + 1):
        # 计算方程两边的差值
        left_side = x_int + y
        right_side = math.sqrt(x_int ** 2 - 111) + 12
        diff = abs(left_side - right_side)

        # 找到差值最小的 x 值的整数区间
        if diff < min_diff:
            min_diff = diff
            best_x_int = x_int
        else:
            break

    min_diff = float('inf')

    # 在 best_x_int 的附近以步进 0.001 的方式带入 x
    for x in range(int((best_x_int -2) * 1000), int((best_x_int + 2) * 1000)):
        x_val = x / 1000.0
        left_side = x_val + y
        right_side = math.sqrt(x_val ** 2 - 111) + 12
        diff = abs(left_side - right_side)

        # 找到最小的差值对应的 x 值
        if diff < min_diff:
            min_diff = diff
            best_x = x_val
        else:
            break
    else:
        if min_diff >= 0.01:
            return -1

    return round(best_x, 2)


# 给定 y 值
# y = 11.4  # 你可以根据需要修改 y 的值

# 值少于 10 个字符用空格填充 (冒号小于号之间的字符)
print("{: <10}|{: <10}".format("x", "y"))

# 计算并输出 x 的最小可能值
for i in range(100, 121):
    x_min = find_min_x(i/10)
    print("{: <10}|{: <10}".format(x_min, i/10))

输出:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

x         |y         
28.75     |10.0      
30.16     |10.1      
31.73     |10.2      
33.5      |10.3      
35.49     |10.4      
37.75     |10.5      
40.34     |10.6      
43.34     |10.7      
-1        |10.8      
-1        |10.9      
-1        |11.0      
-1        |11.1      
-1        |11.2      
-1        |11.3      
-1        |11.4      
-1        |11.5      
-1        |11.6      
-1        |11.7      
-1        |11.8      
-1        |11.9      
-1        |12.0      

后记

用上了再说吧, 想着一个小风机或许不需要导轨限位呢 ( ).
不过解决了问题还是很开心的.
超级感谢🐯同学提供的思路🙏.

等等, 为什么没有想到 这是一个可以画图的函数呢?

😭